你有没有想过,那些我们习以为常的图像,比如照片、医学扫描图,背后其实隐藏着复杂的数学变换?今天,我们就来聊聊刚性变换这个话题,看看它是如何让图像变得如此神奇。
刚性变换是什么?
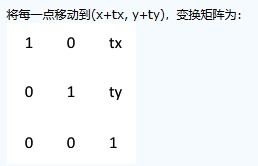
刚性变换,听起来可能有些抽象,但它在实际应用中却无处不在。简单来说,刚性变换是一种保持物体形状不变的几何变换。想象你手里拿着一个积木,无论你如何旋转它,它的形状都不会改变,这就是刚性变换的精髓所在。在数学上,刚性变换包括平移、旋转和缩放,但需要注意的是,缩放并不属于刚性变换的范畴,因为缩放会改变物体的形状。
刚性变换的应用

刚性变换在图像处理中的应用非常广泛。比如,在医学影像中,医生需要将不同设备采集到的影像进行融合,以便更全面地诊断病情。这时候,刚性变换就能派上用场了。通过刚性变换,医生可以将不同影像对齐,从而更容易发现病灶。
再比如,在遥感图像处理中,刚性变换也发挥着重要作用。卫星拍摄的图像往往需要进行对齐,以便进行地形分析。刚性变换能够确保图像在变换后仍然保持原有的形状,从而提高分析精度。
刚性变换的实现
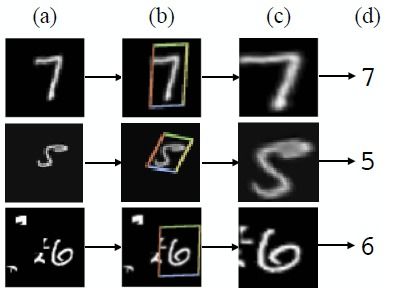
刚性变换的实现通常涉及到复杂的数学计算。在计算机视觉领域,刚性变换通常用矩阵来表示。比如,一个二维刚性变换可以用一个3x3的矩阵来表示,这个矩阵包含了旋转和平移的信息。
具体来说,一个二维刚性变换可以表示为:
\\[ \\begin{pmatrix} x' \\\\ y' \\\\ 1 \\end{pmatrix} = \\begin{pmatrix} \\cos \\theta & -\\sin \\theta & t_x \\\\ \\sin \\theta & \\cos \\theta & t_y \\\\ 0 & 0 & 1 \\end{pmatrix} \\begin{pmatrix} x \\\\ y \\\\ 1 \\end{pmatrix} \\]
其中,\\( \\theta \\) 是旋转角度,\\( t_x \\) 和 \\( t_y \\) 是平移量。通过这个矩阵,你可以将一个点 \\( (x, y) \\) 变换为 \\( (x', y') \\)。
刚性变换的挑战
刚性变换虽然听起来简单,但在实际应用中却面临着不少挑战。首先,如何准确地估计刚性变换参数就是一个难题。在图像处理中,通常需要通过优化算法来估计这些参数。比如,可以使用模拟退火算法或鲍威尔算法来找到最优的变换矩阵。
其次,刚性变换只适用于形状不变的物体,但对于一些复杂的图像,比如医学影像,可能需要进行非刚性变换。非刚性变换比刚性变换要复杂得多,但它能够更好地处理图像中的形变。
刚性变换的未来
随着计算机视觉和图像处理技术的不断发展,刚性变换的应用将会越来越广泛。未来,刚性变换可能会在更多的领域发挥作用,比如自动驾驶、机器人视觉等。同时,随着算法的不断改进,刚性变换的精度和效率也将会得到进一步提升。
刚性变换虽然是一个看似简单的概念,但在实际应用中却蕴含着巨大的潜力。通过不断探索和创新,刚性变换将会在更多的领域发挥重要作用。





